データ分析の目的としてよくあらわれる手法が分類です．今回のコラムでは，すでに分類が既知であるデータ（教師ありデータ）を想定していますので，階層的クラスタリングのような未知の分類を行う問題のことではないので注意してください．
分類をする統計モデルといえば樹形モデル（決定木）が有名ですが，企業の倒産確率を出すモデルや手術の成功確率を出すモデルなども，倒産するか否か，手術が成功するか否かという確率を通じてサンプルを2群に分けているので，ある種の分類をしているモデルになります．このような分類のモデルは，本学の学生のレポートや論文，さらには技術指導をしている企業のデータ分析でもよく使われているのですが，その分類性能を上げるために，多くの場合，新たな説明変量を加えたり，外したりという作業に注力しているように見えます．そして，p値が0に近く統計的に有意になればその説明変量を採用し，分類の限界性能を追求しているようなケースが多いように思われます．
このようなやり方も全くの誤りというわけではありませんが，実はもっと簡単な方法があります．それが箱型図の視覚化です．次の図は，脊椎側弯症という背骨の病気の手術結果のデータから作成した箱ひげ図（箱型図）です．左側の箱は，背骨の特定の位置(Start)に対して手術を行った結果，症状が消えた（absent）人たちの標本分布であり，右側の箱は症状が残った（present）人たちの標本分布です．このような分類ごとの箱ひげ図の描画のことを，探索的データ解析では「条件付き箱ひげ図」と呼びます．
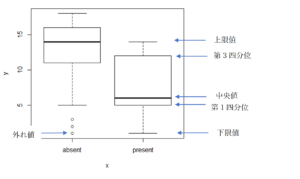
箱ひげ図の読み方については他の参考書にゆずり，ここでは簡単な説明にとどめますが，１つの箱ひげ図は1変量データの分布を表しており，上限値から下限値の間に大半のデータの値が収まり，第3四分位と第1四分位で囲まれた箱が小さいほど中央値付近に値が集中していることを意味します．この図の場合，手術を成功した人はほぼ Start の位置が大きい番号であり，失敗した人はStartの位置が小さい番号であるという傾向が読み取れます．そして分布のレンジ自体も上下にずれていることから，手術の成否に対して Start は大きく寄与している可能性が高いことがわかります．
このように図で分類の効果がわかるデータは，統計モデルに変量として用いてもそのp 値はとても小さいです．以下は，先のデータの手術の成否確率をあらわす一般化線形モデルをRであてはめた結果の一部を抜粋しています．Start のPr(>|z|)がp値をしめしていますが，非常に0に近く有意であることがわかります．
このような条件付き箱ひげ図を習慣的に描くようになるとわかるのですが，分類に対して効果のある変量はおしなべて分布の中心も，そのレンジも大きくずれています．言い換えれば，モデルをあてはめなくとも，箱ひげ図のデータを眺めるだけで分類に有効な変量というのは拾い上げることができるというわけです．また，箱ひげ図があまりずれていないようであればp値はそれほど小さくならず，仮に判断に迷うようなp値（0.1くらい）だったとしても，条件付き箱ひげ図において比較する標本分布にずれが生じていないようであれば，私の過去の経験ではありますが，その変量を採用しない方が無難なことが多かったです．加えて，私の本務校で取り上げられる金融データでも，M&Aの成否，倒産と非倒産，戦略的株式非公開の実施の有無，企業の格付けなど分類を扱う問題は数多くありますが，分類の成功するモデルで使われる変量の条件付き箱ひげ図はいつも大きくずれていました．モデルをあてはめて形式的な数値を眺める分析もそれはそれで意味のある事ですが，このようなグラフィカル表現では，外れ値の存在が一目でわかるなどの副次的な効果も非常に高いので，皆さんもぜひ使ってみてはいかかでしょうか．