実務であれ、学術の世界であれ、２つの変量（データの列）の間に相関（何らかの関係）があるかを調べるときに最もよく使われている２つの道具といえば、相関係数と単純線形回帰モデルでしょう。下手をすればそれ以外の道具は使わない、使ったことがないという方もいるくらいですから、その結果が及ぼす影響力は大変大きなものになります。
2つの道具の背景を簡単に説明します。２つの変量をそれぞれx,yとしますと、相関係数はcov(x,y)/√(var(x)) √(var(y))という値であり、単純線形回帰モデルとはy=α+βx+εという線形式になります。ここでεは誤差を表します。相関係数を使って実際に相関があるか判断するときは、それぞれの変量に対応する2つのデータ列から共分散cov(x,y)と分散var(x),var(y)の値を推定し、先の相関係数の式に代入して求めます。1の値に近ければ正の相関、-1に近かければ負の相関、0に近ければ無相関という判断になります。線形回帰モデルを使った場合は、データからαとβを推定し、それぞれの値が統計的に有意かどうかを調べます。具体的には推定したβの値が0でないと判断された場合（推定したβに関するp値が0に近い場合）に2つの変量に線形の関係があると考えます。
以上のように説明を書くととてもややこしい話に聞こえますが、相関係数や線形回帰モデルの推定は、表計算ソフトやフリーの統計ソフトを使えばコマンド1つで計算できるので、実は数学を全く理解していなくても簡単に計算できます。おそらくデータ分析の入門書には必ず出てくる内容です。そのため、使い方だけを覚えて相関の有無を判断している人を多く見かけます。しかしながら、上の2つの道具は次の図1に存在する明らかな相関関係を見つけることはできません（図１の計算に用いたデータはこのリンクからダウンロード可能です）。
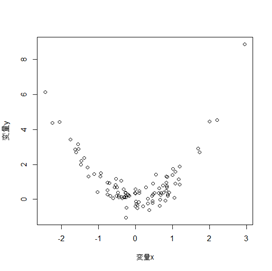
図1 散布図
人間の目で見れば明らかに非線形関係（おそらく2次関数）が見て取れますが、相関係数の推定値は-0.057 と限りなく0に近く、線形回帰モデルのβの推定値は-0.088でそのp値は0.57と０よりもかなり大きいです（脚注：多くの分析では0.05 以下のp値であれば有意とします。0.1よりも大きな値を閾値にすることはほとんどありません。）。2つの道具は、あくまで2つの変量の線形性を測る道具なのでこのような見逃しは当然の結果ではありますが、やはり2つの道具の影響力が大きいため、このような誤りは学生のレポートだけでなく、学会発表や実務のデータ分析でもしばしば見受けられます。ちなみに、このデータで2次の関係の有無があるかを調べる場合は、変量xに相当するデータを先に2乗しておき、線形回帰モデルに当てはめればよいだけです。この例では、βはおよそ1、p 値もおよそ0という結果になりました。
昨今では相関よりも一歩踏み込んだ因果にまで立ち入ってその有無を推定する統計手法が開発されました。しかしながら、それはやはり線形関係の発見の延長でしかなく、この例のような非線形な関係まではどうしても見つけられません。道具に当てはめる前に散布図を描いて眺めておけば、このような問題は簡単に避けられます。高度な統計モデルや統計手法にデータを当てはめる前に、一度、データのグラフィカルな調査をしてみてはいかがでしょうか。